In total I probably spent 30 hours on this set, and half of that time was refactoring some previous functions I wrote in previous challenges.
With the completion of this set, I’ve officially caught up to my freshman self, hopefully with a bit more mature coding style.
Set 3 Challenge 1 (Number 17): The CBC padding oracle
Puzzle
This is the best-known attack on modern block-cipher cryptography.
Combine your padding code and your CBC code to write two functions.
The first function should select at random one of the following 10 strings:
MDAwMDAwTm93IHRoYXQgdGhlIHBhcnR5IGlzIGp1bXBpbmc=MDAwMDAxV2l0aCB0aGUgYmFzcyBraWNrZWQgaW4gYW5kIHRoZSBWZWdhJ3MgYXJlIHB1bXBpbic=MDAwMDAyUXVpY2sgdG8gdGhlIHBvaW50LCB0byB0aGUgcG9pbnQsIG5vIGZha2luZw==MDAwMDAzQ29va2luZyBNQydzIGxpa2UgYSBwb3VuZCBvZiBiYWNvbg==MDAwMDA0QnVybmluZyAnZW0sIGlmIHlvdSBhaW4ndCBxdWljayBhbmQgbmltYmxlMDAwMDA1SSBnbyBjcmF6eSB3aGVuIEkgaGVhciBhIGN5bWJhbA==MDAwMDA2QW5kIGEgaGlnaCBoYXQgd2l0aCBhIHNvdXBlZCB1cCB0ZW1wbw==MDAwMDA3SSdtIG9uIGEgcm9sbCwgaXQncyB0aW1lIHRvIGdvIHNvbG8=MDAwMDA4b2xsaW4nIGluIG15IGZpdmUgcG9pbnQgb2g=MDAwMDA5aXRoIG15IHJhZy10b3AgZG93biBzbyBteSBoYWlyIGNhbiBibG93
… generate a random AES key (which it should save for all future encryptions), pad the string out to the 16-byte AES block size and CBC-encrypt it under that key, providing the caller the ciphertext and IV.
The second function should consume the ciphertext produced by the first function, decrypt it, check its padding, and return true or false depending on whether the padding is valid.
Solution
While I think Wikipedia explains it incredibly well, I’ll give an attempt at explaining as well.
Recall that PKCS7 padding works by making sure the last n bytes of a message are equal to n itself. Our decryption oracle does this checking for us. Recall also from the previous challenge that we saw how we could influence the next block’s plaintext bytes by changing the current ciphertext block’s same respective byte. The only difference is that we don’t know the plaintext’s byte– but we can infer it from just making 256 requests with crafted ciphertext, and also using the oracle which tell us if padding is correct or not.
This idea can be expressed as follows:
for guessed_byte in range(256):
crafted_ciphertext = old_ciphertext[:14] + guessed_byte
// where guessed_byte represents our crafted ciphertext byte from the previous block
plaintext_i = decrypt_oracle(crafted_ciphertext)
// Within the oracle, this will happen:
// plaintext_i[15] = aes_i[15] ⊕ guessed_byte
// and all the other plaintext bytes will remain the same.
check_padding(plaintext_i)
The code above will keep probing and computing plaintext_i and the check_padding function will see if plaintext_i is padded correctly, i.e. if it ends in “0x01”.
Once the padding verifier returns “valid”, we then easily know the value of aes_i[15] since plaintext_i[15] == 0x01 and we control guessed_byte.
We can then keep extending this idea and move on to the next byte: Now our goal is to make plaintext_i end in some padding like \x02\x02.
We can make plaintext_i[15] = \x02 since we know aes_i[15], and we can figure out aes_i[14] by using the same function above, but using a crafted byte to make the last plaintext byte fit the padding we want (i.e. \x02) before sending the ciphertext off to the oracle.
for guessed_byte in range(256):
crafted_ciphertext = old_ciphertext[:13] + guessed_byte + prev_byte
// where prev_byte is crafted to force the plaintext to equal 0x02
plaintext_i = decrypt_oracle(crafted_ciphertext)
// At some point, plaintext_i[14] = aes_i[14] ⊕ guessed_byte === 0x02
check_padding(plaintext_i)
Thus, inevitably, the guessed_byte will result in some plaintext_i that returns valid padding, at which point we know the value aes_i[14]. Keep repeating the process– set the last 3 bytes of the crafted ciphertext to 0x03 (which we can compute since we derived aes_out[14] and aes_out[15]) and probe for aes_out[13]– until the whole block is enumerated, and keep going through every block in the message until all AES state is enumerated.
There were a handful of false positives that made this challenge take a bit longer for me. For instance, it is possible that some byte of aes_out may genuinely decrypt to whatever padding value we injected. This would happen if we attempted to decrypt the last block of a message, which is genuinely padded. For instance, if aes_out[15] decrypts to \x01 under normal circumstances, our formula would simply return guessed_byte as being \x00, which we don’t know if it’s a genuine
correct guess, or just a result of the edge case. From the way I’ve constructed the loop, it will spit out 2 results as the “correct guessed byte”.
In this case, I simply attempt the next iteration as normal with one of the bytes, and if that succeeds I know it’s correct, and if it doesn’t I know the other result was the correct byte.
One might ask themselves, “what if aes_out[14] just happens to decrypt to \x02 normally?” which is a perfectly valid point, and is a scenario I purposefully ignored for simplicity– 1) it’d be a pain to keep track of up to 15 bytes for some event that’s reasonably unlikely and 2) The plaintext is largely known to be of some form of English, and it’s even more unlikely that some PKCS7 padded English would end in \x02.
This challenge is incredibly similar to the previous challenge (Challenge 16), but was still fun and definitely realistic. This challenge probably took the most time out of the set. Code for this set is on my Github.
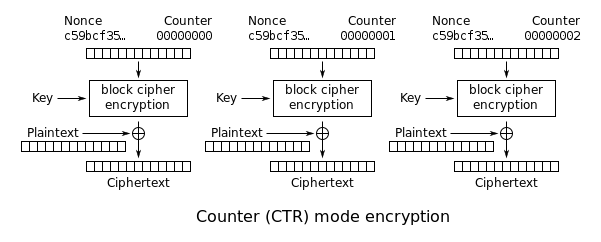
Set 3 Challenge 2 (Number 18): Implement CTR, the stream cipher mode
Puzzle
The string:
L77na/nrFsKvynd6HzOoG7GHTLXsTVu9qvY/2syLXzhPweyyMTJULu/6/kXX0KSvoOLSFQ==… decrypts to something approximating English in CTR mode, which is an AES block cipher mode that turns AES into a stream cipher, with the following parameters:
key=YELLOW SUBMARINEnonce=0format=64 bit unsigned little endian nonce,64 bit little endian block count (byte count / 16)CTR mode is very simple.
Instead of encrypting the plaintext, CTR mode encrypts a running counter, producing a 16 byte block of keystream, which is XOR’d against the plaintext.
For instance, for the first 16 bytes of a message with these parameters:
keystream = AES("YELLOW SUBMARINE","\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00")… for the next 16 bytes:
keystream = AES("YELLOW SUBMARINE","\x00\x00\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00\x00\x00\x00\x00")… and then:
keystream = AES("YELLOW SUBMARINE","\x00\x00\x00\x00\x00\x00\x00\x00\x02\x00\x00\x00\x00\x00\x00\x00")CTR mode does not require padding; when you run out of plaintext, you just stop XOR’ing keystream and stop generating keystream.
Decryption is identical to encryption. Generate the same keystream, XOR, and recover the plaintext.
Solution
I feel this is pretty straightfoward. The explanation is clear enough. Below is the primary core of the cipher’s operation.
while block:
ctr_data = pack('<QQ', int(nonce, 16), ctr) # see struct library for packing formatting
aes_out = aes_ecb_encrypt_with_key(ctr_data, bytes.fromhex(key))
ctr_output += xor_hex_strings(aes_out[0].hex()[:len(block)], block)
ctr += 1
block = data[ctr*32:(ctr+1)*32]
Simply keep an internal counter in the while loop and encrypt that with the nonce and call it a day. Assuming you keep the nonce secret and don’t reuse it, nobody should be able to predict the outputted AES state.
…which is a nice segue into our next challenge!
Set 3 Challenge 3 (Number 19): Break fixed-nonce CTR mode using substitutions
Puzzle
Take your CTR encrypt/decrypt function and fix its nonce value to 0. Generate a random AES key.
In successive encryptions (not in one big running CTR stream), encrypt each line of the base64 decodes of the following, producing multiple independent ciphertexts:
(This should produce 40 short CTR-encrypted ciphertexts).
Because the CTR nonce wasn’t randomized for each encryption, each ciphertext has been encrypted against the same keystream. This is very bad.
Understanding that, like most stream ciphers (including RC4, and obviously any block cipher run in CTR mode), the actual “encryption” of a byte of data boils down to a single XOR operation, it should be plain that:
CIPHERTEXT-BYTE XOR PLAINTEXT-BYTE = KEYSTREAM-BYTEAnd since the keystream is the same for every ciphertext:
CIPHERTEXT-BYTE XOR KEYSTREAM-BYTE = PLAINTEXT-BYTE (ie, "you don't say!")Attack this cryptosystem piecemeal: guess letters, use expected English language frequence to validate guesses, catch common English trigrams, and so on.
Solution
Just to be upfront– I did not complete this challenge as I found it too much to be a pain in the ass. All the manual work that is required is tremendous, and too tedious for my liking. I actually skipped ahead to the next challenge where you do this in a much more automated way.
I didn’t fully understand the point of this exercise, other than being a slightly gentler introduction as to how CTR works/can be misused compared to the next challenge. In any case, here is what I believe they were trying to get people to think about.
As the problem says, because the same nonce is used in every operation, we can simply issue crafted ciphertexts in a similar manner to challenge 17 to try and discover the “keystream byte”. We can probe 256 times for every ciphertext byte and examine the decrypted output and try to run frequency analysis. My initial code looked something like this:
for guessed_byte in range(256):
ciphertext = ciphertext_old[:15] + guessed_byte // slice the last byte and replace with my guess
plaintext = aes_ctr_operation(ciphertext)
analyse_plaintext(plaintext)
Where the analyse_plaintext function would, as the name implies, do some frequency analysis on the string to see if it “made sense” for English. Done for the whole list of ciphertexts, I believe the challenge wanted us to do manual work like this (a gif which I blatently stole from here)
In my attempt to automate this, I went down a bit of a rabbit hole. I noticed my analyse_plaintext function wouldn’t work very well for a single decrypted byte, since the other 15 bytes of a decryption would still be gibberish, so I had attempted to group things together, instead trying to probe 4 letters at a time and analysing those 4 decrypted bytes. However, this got very tedious as it resulted in 2564 operations for a 4 byte block, which had to be done 4 times (since 16
bytes in a block). The run time for this is astronomical, as after 30 minutes I hadn’t even finished one blocks.
I believe I fully understood the concepts they were trying to teach (especially since I completed the next challenge anyways) but the method of teaching was a little too tedious for me. I think what would’ve made the challenge better and far less manual would be to provide some known plaintexts for every ciphertext and then, once the keystream bytes are figured out, decrypt other ciphertexts using that same knowledge. This would make detection of what a “correctly guessed byte” far simpler while still demonstrating how using a fixed nonce is bad.
In any case, I apologize for any reader that was looking forward to some code for this, but as the challenge even states, it’s a pretty inelegant, manual, rough solution. Hopefully my explanation of the process of what one should do is suffice; otherwise, go look at the blog I linked above!
My attempted code is still on the Github, but not recommended to try and run it.
Set 3 Challenge 4 (Number 20): Break fixed-nonce CTR statistically
Puzzle
In this file find a similar set of Base64’d plaintext. Do with them exactly what you did with the first, but solve the problem differently.
Instead of making spot guesses at to known plaintext, treat the collection of ciphertexts the same way you would repeating-key XOR.
Obviously, CTR encryption appears different from repeated-key XOR, but with a fixed nonce they are effectively the same thing.
To exploit this: take your collection of ciphertexts and truncate them to a common length (the length of the smallest ciphertext will work).
Solve the resulting concatenation of ciphertexts as if for repeating- key XOR, with a key size of the length of the ciphertext you XOR’d.
Solution
This challenge is incredibly similar to the one from Set 1 Challenge 6 where we broke repeating key XOR, except only this time instead of a literal key, it’s a keystream (the output of the AES cipher). In fact, it’s so similar, the code required for this attack was literally copied-and-pasted from Set 1 Challenge 6, with the only adjustment being removing the block size detection functionality (since we know it’s AES, making the block size 16) and fixing it to be the found shortest length of the given file.
Here’s a short recap of Set 1 Challenge 6, and how it is easily extendible to this challenge now.
In Set 1 we were provided a message within a file that was encrypted with repeating-key XOR, so basically every key_len bytes of the plaintext were XOR-d against the key. This meant that the message was essentially broken up into msg_len/key_len blocks, where msg[0], msg[key_len], msg[key_len*2] and so on were encrypted the same exact way– that is, XOR-d with key[0].
Assuming the message is simply English plaintext, we can line up msg[0], msg[key_len], msg[key_len*2] and brute force what key[0] might be by probing all possible 256 bytes of key[0] and run frequency analysis on that decrypted text.
Taking a look at CTR, it really is the exact same situation if you take away the whole “block cipher encryption” block and only focus on the inputs to the XOR function. Besides the keystream difference, another difference is that there are multiple messages for us to transpose and “line up” for analyzing, but there isn’t much difference between “one message” and “multiple messages” in terms of handling the data.
This is why the challenge recommends we find some “common length”, which was recommended to be the shortest length ciphertext, since we know that the all the first shortest_ciphertext_len keystream bytes are the same for every ciphertext due to the nature of AES-CTR. For ciphertexts longer than that, it would be as simple as finding the next “common length” and excluding the previously “shortest ciphertext”.
All in all, a far better and more scalable way to decrypt ciphertext than the previous challenge. I always love automating things.
On my github you’ll see incredibly similar code to this challenge at Set 1 Challenge 6 so I don’t see much point in posting bits of core code. In hindsight I probably should’ve made it an easy to use function, but I got slightly lazy :)
Set 3 Challenge 5 (Number 21): Implement the MT19937 Mersenne Twister RNG
Puzzle
You can get the psuedocode for this from Wikipedia.
If you’re writing in Python, Ruby, or (gah) PHP, your language is probably already giving you MT19937 as “rand()”; don’t use rand(). Write the RNG yourself.
Solution
Pretty straightforward. Just do it since its pretty easy to read the pseudocode.
I likely should have implemented these functions in a class instead of global variables and functions, which I may very well do in the future if this messy code really truly does bother me (which it kinda does right now…). After all it’s pretty messy if one may want multiple instances of a random object; however, this “global seeding” is how many implementations provide their interface anyways, which is what I first had in mind when implementing.
I validated my solution from this person’s Github, though of course I still don’t know how “to spec” my code is. Nevertheless, I don’t think the “quality” of the numbers matters too much, rather the point is to show “why rand() is insecure” in the future challenges :)
Set 3 Challenge 6 (Number 22): Crack an MT19937 seed
Puzzle
Make sure your MT19937 accepts an integer seed value. Test it (verify that you’re getting the same sequence of outputs given a seed).
Write a routine that performs the following operation:
Wait a random number of seconds between, I don’t know, 40 and 1000. Seeds the RNG with the current Unix timestamp Waits a random number of seconds again. Returns the first 32 bit output of the RNG.
You get the idea. Go get coffee while it runs. Or just simulate the passage of time, although you’re missing some of the fun of this exercise if you do that.
From the 32 bit RNG output, discover the seed.
Solution
Also reasonably straightforward. Because we know it’s a 32 bit timestamp, and we “know” our previously seeded RNG is seeded with some previous timestamp so it’s simple to just enumerate previous values (Since 32-bits result in ~4 billion possible values, which really isn’t that much since processors can easily run 4GHz+).
From there, for every new seed we provide, we can simply call extract_number and check that value against the received value.
For the sake of easy development and iteration, I simply “jumped ahead” in time by polling the current time and adding a random number, and doing it again. This is basically “taking the magic away” as they say it, but I value development time more than “realism” I suppose :) .
Obviously this can just be done in a for loop, where there’s some setup to forge a time, and then in the actual loop we can keep decrementing from the current time until we find a match between our guessed seed value and the original value.
All in all, pretty easy, but a nice short demonstration of what to be cautious for using rand().
Set 3 Challenge 7 (Number 23): Clone an MT19937 RNG from its output
Puzzle
The internal state of MT19937 consists of 624 32 bit integers.
For each batch of 624 outputs, MT permutes that internal state. By permuting state regularly, MT19937 achieves a period of 219937, which is Big.
Each time MT19937 is tapped, an element of its internal state is subjected to a tempering function that diffuses bits through the result.
The tempering function is invertible; you can write an “untemper” function that takes an MT19937 output and transforms it back into the corresponding element of the MT19937 state array.
To invert the temper transform, apply the inverse of each of the operations in the temper transform in reverse order. There are two kinds of operations in the temper transform each applied twice; one is an XOR against a right-shifted value, and the other is an XOR against a left-shifted value AND’d with a magic number. So you’ll need code to invert the “right” and the “left” operation.
Once you have “untemper” working, create a new MT19937 generator, tap it for 624 outputs, untemper each of them to recreate the state of the generator, and splice that state into a new instance of the MT19937 generator.
The new “spliced” generator should predict the values of the original.
Solution
Pretty classical example of why rand() is not really cryptographically secure, but oftentimes we are “just told” it is, with an explanation along the lines of that the internal state is reversible and ennumerable with 624 accesses. But why?
In my security class in school, we were told this and didn’t go into more detail. I am not criticizing the class for the lack of explanation because, after all, it’s a relatively complex topic to teach a broad undergrad level class where half the students fall asleep anyways. I’m simply saying it’s a similar case to the previous challenges (like breaking the Vignere cipher) where everyone ““knows”” how it works, but might not know the intricate details.
In any case, let’s start “untempering”!
Taking a look at the Wikipedia page, you’ll see that every time a number is “extracted” it the underlying internal state and applies some bitshifts and masks to it before returning it as a number (the shifts and masks being preset numbers according to the algorithm).
if index >= n {
if index > n {
error "Generator was never seeded"
// Alternatively, seed with constant value; 5489 is used in reference C code[48]
}
twist()
}
int y := MT[index]
(4) y := y xor ((y >> u) and d) // where (u, d) = (11, 0xFFFFFFFF)
(3) y := y xor ((y << s) and b) // where (s, b) = (7, 0x9D2C5680)
(2) y := y xor ((y << t) and c) // where (t, c) = (15, 0xEFC60000)
(1) y := y xor (y >> l) // where L = 18
index := index + 1
return lowest w bits of (y)
As the challenge states, we can really generalize the four shifting operations into two operations– shift_right, and shift_left. We should reverse these operations in the above order (1, 2, 3, 4) to obtain the original y internal state value.
Let’s start with the shift_right operation since that’s the first one we need to “reverse” anyways. For the sake of notation, I’ve written the previous y as simply y'. Let’s also use the given value for l just for simplicity.
(1) y := y' ^ (y' >> 18) // 18 == l in the pseudocode
Recall that because this as 32-bit of MT19937, y' >> 18 is essentially a bunch of 0s with the least-significant (32 - 18) or 14 bits as the 14 most significant bits of y'. Written another way in verilog notation which I find easier to understand bitslicing with (since I am a hardware engineer after all!)
assign y = y' ^ {18'b0, y'[31:18]};
(Real quick– for those who don’t know basic syntax. 18'b0 indicates the <bid-width>'<radix><value>, anything between [..] indicates bitslicing, and anything between {..} indicates concatenation.)
Because anything XOR 0 is itself, we can clearly tell that the first 18 (l) bits of y are the same as y' (i.e. y[31:14] == y'[31:14]). Next is just to figure out the least 14 (w-l) bits, which can be expressed as something like this:
y[13:0] == y'[13:0] ^ y'[31:18];
Easy! We know y[13:0] and we know y'[31:14], so just solve for y'[13:0] and we’ve figured out y'.
We can generalize this logic to the other shift_right operation using u and d, since nothing in our “untempering” really depended on the concrete value of the right shift, and d doesn’t really do anything in 32-bit MT19937 (being, after all, just a 32bit mask).
——
Now onto the shift_left operation, which requires a small extra step due to the extra AND operation. Let’s also use some specific values, again just for some simplicity in explaining. I’m skipping step (2) for the moment since I like step (3) to better demonstrate generalizing the problem later.
(3) y := y' ^ ( (y' << 7) & 0x9D2C56800) // for (s, b) = (7, 0x9D2C56800)
Note that our magic number ends in at least s 0s. (Glancing at the magic number for the other left shift, it’s also true that it ends in t 0s.) To be exact, it ends in 11 0s, but we should avoid being completely exact so that it’s easier to generalize later on. In Verilog, considering the inner right shift, our expression might look like this:
y = y' ^ ( {y'[24:0], 7'b0} & {25'h9D2C568, 7'h00);
Because the lowest 7 (s) bits of the magic number are 0, this basically reveals the lowest 7 bits of y' since y[6:0] == y'[6:0] ^ 0, and we know y from the previous step. This is trivial, and now we know y'[6:0].
Now, let’s update our small expression with the new knowledge we obtained:
y = y' ^ ( {y'[24:7], y'[6:0], 7'b0} & {25'h9D2C568, 7'h00} );
We now know a little bit more about our shift value! And it’s quite easy to use it to our advantage. Much like how in (1) we noticed we could “solve” the XOR since we knew two of the values in the expression, we can do the same here if we reduce our expression to something like this:
y[13:7] = y'[13:7] ^ ( y'[6:0] & 7'h68 );
Where we know y[13:7] since it’s a previous number, we know y'[6:0] from the previous step, and we obviously know the magic number because it’s given to us. Thus, we’ve solved y'[13:7]!
We can keep going with this. Because we know y'[13:7] we can learn y'[20:14]; because we can learn y'[20:14] we can learn y'[27:21]; and so on and so forth (up until the word width of course). If we keep “shifting” our “window” of inspection of arbitrary bits it’s reasonably simple.
This approach is reasonably generic, as it’s only “dependency” is having a couple 0s as LSBs in the magic number, but that means this algorithm can be used for the numbers involved with the other shift_left operation (t, c).
And there you have it! You can now brute force any MT19937 implementation. This was reasonably high level, but some of the exact details can obviously be found on Github, as well as some (not really) beautiful comments. I also tested this briefly by seeding my Twister several times and extracting 624 times, checking my extracted number with the state every time.
——
NOTE / MINI-RANT: While solving this I was curious and looked at a couple other solutions to see their approaches. I was, quite frankly, very disappointed (of course, I am heavily biased)– some just referenced old blogs and “adjusted it for their purposes”; some were very handwavy just “calling it magic” and “if you don’t believe me, try it out yourself”; one person just said “screw it” and expressed the operations as a function and threw it into an SMT solver (which, honestly, if I were super lazy I would indeed do). Perhaps the one writeup I really did enjoy was this one that had expressed it quite elegantly and felt very thorough in his explanation.
One quite large pet peeve I have is when someone has solutions to a problem but little explanation around it, which tends to happen with – no flattery intended – incredibly smart people that will skip steps in their mind because it’s “trivial”. I’ve been on both ends– having been both a student and a TA in recent history, I’ve been both confused and the confuser. Still, it’s quite annoying when I’m just told something without me fully understanding why, especially when I read it off a multiple year old blog and can’t easily ask a question.
I find that explaining things is much harder than actually doing “x” thing in the first place (sometimes I’m a bit too wordy even), but still it’s a skill I intend to work on and would like to see the industry emphasize.
Hopefully whoever may stumble across the dozens of Cryptopals writeups already existing finds this writeup helpful instead of overwhelming!
Set 3 Challenge 8 (Number 24): Create the MT19937 stream cipher and break it
Puzzle
You can create a trivial stream cipher out of any PRNG; use it to generate a sequence of 8 bit outputs and call those outputs a keystream. XOR each byte of plaintext with each successive byte of keystream.
Write the function that does this for MT19937 using a 16-bit seed. Verify that you can encrypt and decrypt properly. This code should look similar to your CTR code.
Use your function to encrypt a known plaintext (say, 14 consecutive ‘A’ characters) prefixed by a random number of random characters.
From the ciphertext, recover the “key” (the 16 bit seed).
Use the same idea to generate a random “password reset token” using MT19937 seeded from the current time.
Write a function to check if any given password token is actually the product of an MT19937 PRNG seeded with the current time.
Solution
I wasn’t totally sure what to do with the challenge, especially since a good amount of it was stuff we’d already done.
The encryption is indeed very similar to AES-CTR, the only difference being using extract_number instead of a nonce.
init_seed(key)
keystream = ''
while len(keystream) < len(msg):
keystream += format(extract_number(), '08x')
Decryption is the same operation.
In terms of recovering a key, it’s as simple as brute-forcing because the “key” is only 16 bits, which is a puny keyspace for a key :)
known_plaintext_hex = known_plaintext.encode().hex()
for guessed_key in range(2**16):
if known_plaintext_hex in decrypt(format(guessed_key, '032x'), ciphertext):
return guessed_key
Since we know the plaintext, we can just probe every integer in the keyspace and check if the decrypted text holds some match to our known plaintext (e.g. like the challenge says, 14 ‘A’s). It doesn’t really matter how random the prefix or suffix is.
We can use that same idea for the “password reset”, where the token itself is a sort of “known plaintext” and the time at which the token was generated is the “key”.
With respect to “MT19937 token detection”, we can simply use the function written in Set 3 Challenge 6 to detect MT19937 usage, which will try decrementing the current time and using that as a seed until the entire 16-bit key space is exhausted. If that fails, then we know the password reset token was not generated with MT19937.
Not as fun as the previous challenges, but I do somewhat understand the point of it. These scenarios feel relatively realistic, even if they weren’t as “fun” per se!
Hope you enjoyed this read through! Fun as it was, definitely took a long time to write up. Looking forward to Set 4 (and/or other projects I have in my pipeline ;) ).