I spent 20 hours on this set, but I also didn’t do one challenge since it involved MD4– perhaps I’ll revisit it with some other hash that’s vulnerable to length extension attacks (like SHA2). Overall, this set was (as stated) a bit easier than the last one.
One thing that I learned/found pretty cool was implementing SHA1 myself and really internalizing why length extension attacks were possible. In my security classes we were just told about “internal state” without getting into much detail about it.
Set 4 Challenge 1 (Number 25): Break “random access read/write” AES CTR
Puzzle
Back to CTR. Encrypt the recovered plaintext from this file (the ECB exercise) under CTR with a random key (for this exercise the key should be unknown to you, but hold on to it).
Now, write the code that allows you to “seek” into the ciphertext, decrypt, and re-encrypt with different plaintext. Expose this as a function, like, “edit(ciphertext, key, offset, newtext)”.
Imagine the “edit” function was exposed to attackers by means of an API call that didn’t reveal the key or the original plaintext; the attacker has the ciphertext and controls the offset and “new text”.
Recover the original plaintext.
Solution
Here we are “exposed” to an API that has a reuses a key and nonce for AES-CTR. Recall how CTR mode works:
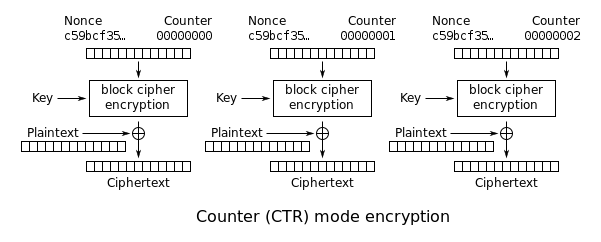
Because the keystream is fixed (much like in previous challenges), the system essentially obeys the below equation:
keystream[i] == orig_plaintext[i] ^ orig_ciphertext[i]
This equation is true for any plaintext and any ciphertext, so if we can calculate the keystream, we can derive the original plaintext (since we possess the original ciphertext).
and we are able to generate our own ciphertexts from the oracle, we are able to reliably derive the keystream by simply sending plaintexts to the oracle, capturing the ciphertexts, and XOR-ing them together like the equation below.
I took advantage of the “API” to simply replace all of the original plaintext with my own plaintext (say, “A”*original_length) to get the new ciphertext. Then, following the above equation, I can just XOR my known plaintext with my new ciphertext from the oracle to get the keystream bytes.
Finally, I can calculate the original plaintext since I’ve derived the keystream, and also know the original ciphertext.
Easy stuff!
Set 4 Challenge 2 (Number 26): CTR bitflipping
Puzzle
There are people in the world that believe that CTR resists bit flipping attacks of the kind to which CBC mode is susceptible.
Re-implement the CBC bitflipping exercise from earlier to use CTR mode instead of CBC mode. Inject an “admin=true” token.
Solution
As the challenge says, it’s incredibly similar to the previous CBC bitflipping challenge. Frankly, it was a bit easier doing this challenge than the previous one.
We know that with CTR one only needs to look at the N-th keystream/plaintext byte to predict the N-th ciphertext byte, so step 1 would be to find where “N” is so we can get the start position for cutting and slicing. This can be done by encrypting the “empty” string (empty in terms of user input) and comparing that ciphertext with any other ciphertext, finding the first byte of difference between them.
Next, we must derive what the keystream bytes are so that we can modulate the ciphertext that gets decrypted to become the plaintext we want. We can do this in the same way we did it in the previous challenge– by simply issuing a plaintext we know and capturing the resulting ciphertext, since the key and nonce in the oracle are fixed.
Finally, we can simply replace the ciphertext bytes at position N with the information obtained above, such that when the oracle decrypts the forged ciphertext, it has the “admin” plaintext, as in the following equation:
forged_ciphertext[i] = desired_plaintext[i] ^ keystream[i]
This works since CTR decryption simply XORs the keystream again with any ciphertext.
Also relatively straightforward stuff– just requires a slight logic change for the new cipher mode.
Set 4 Challenge 3 (Number 27): Recover the key from CBC with IV=Key
Puzzle
Take your code from the CBC exercise and modify it so that it repurposes the key for CBC encryption as the IV.
Applications sometimes use the key as an IV on the auspices that both the sender and the receiver have to know the key already, and can save some space by using it as both a key and an IV.
Using the key as an IV is insecure; an attacker that can modify ciphertext in flight can get the receiver to decrypt a value that will reveal the key.
The CBC code from exercise 16 encrypts a URL string. Verify each byte of the plaintext for ASCII compliance (ie, look for high-ASCII values). Noncompliant messages should raise an exception or return an error that includes the decrypted plaintext (this happens all the time in real systems, for what it’s worth).
Use your code to encrypt a message that is at least 3 blocks long:
AES-CBC(P_1, P_2, P_3) -> C_1, C_2, C_3Modify the message (you are now the attacker):
C_1, C_2, C_3 -> C_1, 0, C_1Decrypt the message (you are now the receiver) and raise the appropriate error if high-ASCII is found.
As the attacker, recovering the plaintext from the error, extract the key:
P'_1 XOR P'_3
Solution
At this point it’s pretty ingrained (in me at least) how CBC works, but recall how decryption is done:

From previous challenges we’ve seen how changes to the ciphertext block N affect the plaintext of block N+1. It’s a pretty logical conclusion then that if we were to force a decryption with a block of all null bytes, we would leak the key bytes for the next block.
As the challenge clearly states, by modifying the message to C_1, C_2, C_3 -> C_1, 0, C_1 and issuing a decryption on that, we know that the “plaintext” P'_3 is the key bytes of C_1. This leads to the equation:
P_1 == IV ^ C_1_aes_bytes == IV ^ P'_3
So thus simply calculating P_1 ^ P'_3 is enough to leak the key. Definitely an easier challenge, though pretty handy they essentially tell you how to do it :)
Set 4 Challenge 4 (Number 28): Implement a SHA-1 keyed MAC
Puzzle
Find a SHA-1 implementation in the language you code in.
Write a function to authenticate a message under a secret key by using a secret-prefix MAC, which is simply:
SHA1(key || message)Verify that you cannot tamper with the message without breaking the MAC you’ve produced, and that you can’t produce a new MAC without knowing the secret key.
Solution
I implemented SHA-1 myself because it was a decent learning opportunity to fully understand some of the weaknesses that are in the algorithm. This largely goes with every system– The best way to know how to break it is to know how to build it.
Anywho, my implementation lies under $cryptopals/set4/sha1.py. I verified it works by comparing the same hashes of random messages and keys with hashlib.
There’s not much to it! The SHA-1 pseudocode is really quite thorough, so it didn’t take much time to do.
Set 4 Challenge 5 (Number 29): Break a SHA-1 keyed MAC using length extension
Puzzle
Secret-prefix SHA-1 MACs are trivially breakable.
The attack on secret-prefix SHA1 relies on the fact that you can take the ouput of SHA-1 and use it as a new starting point for SHA-1, thus taking an arbitrary SHA-1 hash and “feeding it more data”.
Since the key precedes the data in secret-prefix, any additional data you feed the SHA-1 hash in this fashion will appear to have been hashed with the secret key.
To carry out the attack, you’ll need to account for the fact that SHA-1 is “padded” with the bit-length of the message; your forged message will need to include that padding. We call this “glue padding”. The final message you actually forge will be:
SHA1(key || original-message || glue-padding || new-message)(where the final padding on the whole constructed message is implied)
Note that to generate the glue padding, you’ll need to know the original bit length of the message; the message itself is known to the attacker, but the secret key isn’t, so you’ll need to guess at it.
This sounds more complicated than it is in practice.
To implement the attack, first write the function that computes the MD padding of an arbitrary message and verify that you’re generating the same padding that your SHA-1 implementation is using. This should take you 5-10 minutes.
Now, take the SHA-1 secret-prefix MAC of the message you want to forge — this is just a SHA-1 hash — and break it into 32 bit SHA-1 registers (SHA-1 calls them “a”, “b”, “c”, &c).
Modify your SHA-1 implementation so that callers can pass in new values for “a”, “b”, “c” &c (they normally start at magic numbers). With the registers “fixated”, hash the additional data you want to forge.
Using this attack, generate a secret-prefix MAC under a secret key (choose a random word from /usr/share/dict/words or something) of the string:
"comment1=cooking%20MCs;userdata=foo;comment2=%20like%20a%20pound%20of%20bacon"Forge a variant of this message that ends with “;admin=true”.
Solution
As taught in many security classes, we’re always told length extension attacks are possible because of some “internal state”. The wikipedia explanation elaborates a bit more on the technical details, but never really solidified until implementing the vulnerable primitive myself.
The wikipedia article really is fantastic, but I’ll still explain briefly in my own words how the attack works.
As the challenge states, our system prepends a secret key to whatever input message and some padding. The challenge expresses this as the following:
SHA1(key || original-message || glue-padding)
One can simply see FIPS 180-4 for the exact padding, but the critical part is that it’s padded with the length of the total message for that block and looks similar to this:
b"Pomeranian's\ncomment1=cooking%20MCs;userdata=foo;comment2=%20like%20a%20pound%20of%20bacon\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02\xd0"
Which apparently has a key of Pomeranian's\n and uses the message/cookie given to us in the challenge. Together, the key + message equal 720 bits, seen appended as \x02\xd0 above.
The key insight here is that many web servers will use a key character as a delimiter– websites use &, and this example uses ;. What if, though, we send the padded message as is, i.e. literally set
comment2=%20like%20a%20pound%20of%20bacon\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02\xd0
Then it would become hashed as its own message as well and create a new 512-bit block to be processed, and the corresponding MAC would still be considered valid.
Now suppose we forge a message with ;admin=true– we would want some variation of the cookie like this:
comment2=%20like%20a%20pound%20of%20bacon\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02\xd0;admin=true
This data would result in the parameter “comment2” being set to %20like%20a ... ... \x02\d0 and the parameter “admin” being set to true.
First though we would have to vary and tinker with the number of 0s, since our oracle will prepend the secret key. We would want our forged data to be at the start of a new block, since the MAC we do possess came from the previous single original block as well.
Thus, we know the message, and the resulting hash from the first 512-bit block, but we don’t know the key length. We don’t need/care about the key data itself, just the key length, since that will determine where our forged data will start on a block. It is trivial to derive this though– simply brute force and check if the server accepts the MAC!
Thus, from the MAC digest, we can “set” the state and “update” the hash with additional data, once we brute force the key length and align the data we want to add to the SHA block boundary.
As the challenge says– conceptually, it’s a little tough, but practically, it can be done in less than 5 lines of code.
for guess_key_len in range(128):
crafted_msg = pad_msg(b"A"*guess_key_len + known_msg.encode(), (guess_key_len + len(known_msg))*8)[guess_key_len:] + inject_data
(a, b, c, d, e) = struct.unpack('>5I', bytes.fromhex(original_hash))
forged_mac = sha1(inject_data, (guess_key_len + len(crafted_msg))*8, a, b, c, d, e)[2:]
if validate_mac(crafted_msg, forged_mac):
return forged_mac, crafted_msg
Set 4 Challenge 6 (Number 30): Break an MD4 keyed MAC using length extension
Puzzle
Second verse, same as the first, but use MD4 instead of SHA-1. Having done this attack once against SHA-1, the MD4 variant should take much less time; mostly just the time you’ll spend Googling for an implementation of MD4.
Solution
Honestly, I just skipped this. I saw little need to do it on a hash primitive nobody uses anymore (hopefully), that also uses basically the exact same concept, the only difference being the digest length.
More interesting would be breaking a SHA-2, in that case I would implement SHA-2 as well. Again, even with that, it uses the same concept as the length extension attack.
Sorry if this disappoints anyone– I aim to get back to this challenge and do it using SHA-2 in the future, largely just to implement SHA-2 myself, like how I implemented SHA-1, so I can learn from it.
Set 4 Challenge 7 (Number 31): Implement and break HMAC-SHA1 with an artificial timing leak
Puzzle
The psuedocode on Wikipedia should be enough. HMAC is very easy.
Using the web framework of your choosing (Sinatra, web.py, whatever), write a tiny application that has a URL that takes a “file” argument and a “signature” argument, like so:
http://localhost:9000/test?file=foo&signature=46b4ec586117154dacd49d664e5d63fdc88efb51Have the server generate an HMAC key, and then verify that the “signature” on incoming requests is valid for “file”, using the “==” operator to compare the valid MAC for a file with the “signature” parameter (in other words, verify the HMAC the way any normal programmer would verify it).
Write a function, call it “insecure_compare”, that implements the == operation by doing byte-at-a-time comparisons with early exit (ie, return false at the first non-matching byte).
In the loop for “insecure_compare”, add a 50ms sleep (sleep 50ms after each byte).
Use your “insecure_compare” function to verify the HMACs on incoming requests, and test that the whole contraption works. Return a 500 if the MAC is invalid, and a 200 if it’s OK.
Using the timing leak in this application, write a program that discovers the valid MAC for any file.
Solution
A pretty classic attack that’s been around for decades, it’s also pretty easy to implement, but conceptually a bit harder to understand.
In the challenge we’re given an API where we request a file and provide the keyed HMAC signature of that file. Theoretically, if we don’t have the key, we couldn’t generate the signature. We can, though, due to how the comparison function is implemented.
Time for a TL;DR of timing attacks!
Code, obviously, takes time, and some paths of execution take longer than others, like the case of a branch path. Taking the comparison function we’re told to implement:
for a, b in zip(str1, str2):
if a != b:
return 0
time.sleep(0.05)
return 1
Clearly we do a loop over every character of str1 and str2 and do comparisons such that if a != b, we immediately return a failure, otherwise we move on to check the next character of both strings. Because of the “sleep”, the time it takes to move on to the next character takes a noticeable amount of time.
For example, suppose the signature is cbd719c2ca579c2740a28eb257dcc1ab68e4b85e. Below are the 3 highest and lowest response times from the server when I tried guessing the byte cb:
(189, 0.001232), 0xbd
(188, 0.001239), 0xbc
(190, 0.00125) 0xbe
...
(228, 0.009585), 0xe4
(13, 0.01177), 0x0d
(203, 0.054275) 0xcb
The outlier is clearly the last response time, and by a clear margin. All the other response times are far below the last one, solely because of the sleep timer, and because of this outlier, we definitely know the correct guess of the first byte would be cb.
Continuing this trend, we can also try to brute force the next byte, d7. Below are again the 3 highest and lowest response times from the server with the signature cb**... where ** are our guesses.
(134, 0.052358), 0x86
(145, 0.052772), 0x91
(114, 0.052861) 0x72
...
(211, 0.065354), 0xd3
(223, 0.065462), 0xdf
(215, 0.104404) 0xd7
Again you can see a clear outlier, which indicates that our guess d7 did indeed “sleep” and was a correct guess.
This can be done for the rest of the signature– simply keep guessing and find the outlier that had the longest timing response.
The mitigation for timing attacks is usually to employ constant-time cryptography, i.e. make sure that both execution paths exhibit the same timing behavior, which in this case could be trivially done by just making the other code path “sleep” as well. Of course, this has its faults– there are more ways to exploit execution differences than just time (power, E&M, noise to name a few), but that’s another set of challenges and another threat model!
Set 4 Challenge 8 (Number 31): Break HMAC-SHA1 with a slightly less artificial timing leak
Puzzle
Reduce the sleep in your “insecure_compare” until your previous solution breaks. (Try 5ms to start.)
Now break it again.
Solution
As you may have guessed, real world code won’t have an easy “sleep” to exploit. In the above example, if we remove the sleep function, there would be a single instruction cycle between the two execution paths, which is barely above noise. For me, the code used in the previous challenge “breaks” when the sleep timer is ~0.01.
This can be easily remedied by simply collecting more samples and averaging the response times from each of them. This is just typical statistical analysis to try and get the outlier.
I managed to get the sleep timer down to 0.000001 seconds when I just collect 100 samples and still reliably exfiltrate a signature. Assuming a 1GHz processor, that equates to about 1000 cycles of deviation between the two execution paths. Imagine if we had some “real” code instead of a sleep– 1000 cycles isn’t very much time relatively speaking, equating to a couple cache misses and maybe a few dozen-to-hundred instructions.
Even this still is a toy example. Real world timing attacks often collect thousands or tens of thousands of samples, exploiting single-digit cycle variations, which just goes to show how much of a scary threat timing attacks can be. Even the tiniest timing variation can be exploited with some ingenuity. (Sometimes attackers can “widen” the timing variation with very crafty techniques.)
Fun stuff!
I’ve seen only a handful of writeups that got to set 4, so that’s pretty neat. This writeup took a while since I got sidetracked on a couple other projects, but glad to have gotten it done!